Aquí comienza una serie de artículos en los que se pretende hacer un recorrido por los principios básicos de la Computación Cuántica. Y como la mejor forma de aprender es hacerlo de forma práctica, vamos a acercarnos a este paradigma empleando Qiskit, el framework que ofrece IBM para desarrollar algoritmos que se aprovechen de las particularidades que ofrece la física cuántica aplicada a la computación.

Comencemos por la pregunta más obvia. ¿Cuál es la principal diferencia entre la Computación Clásica y la Computación Cuántica?

Para abordar esa pregunta vamos a comenzar viendo cómo se almacena la información y cómo se tratan las distribuciones de probabilidad en Computación Clásica para en un siguiente artículo confrontarlo con la forma de trabajar en Computación Cuántica.

Distribuciones de Probabilidad en Computación Clásica

Un primer aspecto diferenciador es cómo se representa la unidad mínima de información. En Computación Clásica, la que se emplea para la arquitectura y el software presente en los servidores, ordenadores de sobremesa, portátiles, dispositivos móviles, el procesamiento de información se realiza manipulando bits, de forma que un bit es un fragmento de información que puede tomar o bien el valor 1 o el valor 0, pero sólo uno de esos dos valores.

Dentro de este enfoque, vamos a tratar el tema de distribuciones de probabilidad clásica poniendo el ejemplo del lanzamiento de una moneda que está sesgada. De manera que vamos a representar el resultado de dicho lanzamiento mediante una variable aleatoria X que tomará el valor “0” cuando salga “cara” y el valor “1” cuando se obtenga “cruz”.

Formalmente, por cada lanzamiento de moneda se puede decir que se obtendrá “cara” con una probabilidad P(X=0) = (p_{0}) y “cruz” con P(X=1) = (p_{1}) siendo (p_{i}) >= 0 (es decir la probabilidad de obtener “cara” o de obtener “cruz” será siempre mayor o igual que 0) y (p_{i} = 1).

Vamos a extraer muestras de una distribución aleatoria binomial definida como:

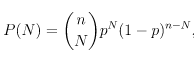donde ‘N’ es el número de éxitos, ‘n’ es el número de intentos y ‘p’ es la probabilidad de éxito en cada intento.

En el siguiente ejemplo el número de intentos será 1 y la probabilidad de éxito (prob_1) será 0.2:

A continuación, podemos comprobar como la suma de las observaciones de 1’s y de 0’s suman 1:

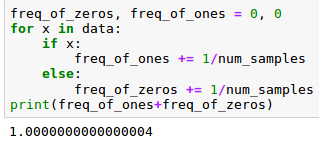
Si queremos representar visualmente (p_{o}) y (p_{1}) veremos que estarán restringidos al cuadrante positivo ya que deben ser mayores o iguales que 0 debido al requisito de normalización. En el siguiente gráfico podemos comprobar como todas las distribuciones de probabilidad del lanzamiento de monedas sesgadas y no segadas caen dentro de la siguiente línea recta del cuadrante positivo:

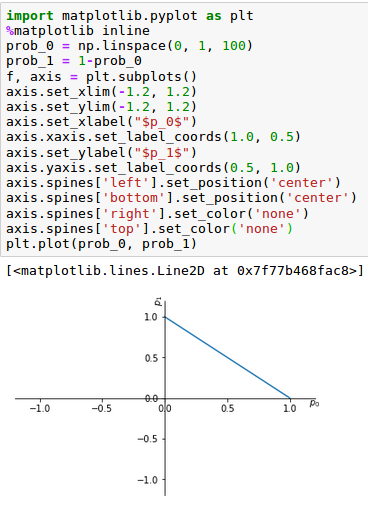
Una forma de representar probabilidades es en forma de vector columnar 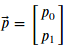, de forma que ponemos una flecha encima del nombre de la variable ‘p’ para diferenciarlo de un escalar. En este caso tenemos un vector representando a una distribución de probabilidad y cuando esto ocurre, recibe el nombre de vector estocástico.

El requisito de normalización indica que la norma del vector está restringida a 1 en la norma (l_{1})lo que se puede expresar como:

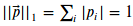
Pero además, como (p_{\text{i\ }})>= 0 estaremos restringidos al cuadrante positivo del círculo unitario. Esto se puede comprobar calculando la norma (l_{1})del vector ‘p’ donde prob_0 = 0.8 y prob_1 = 0.2.

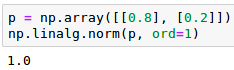
El primer elemento del vector ‘p’ se corresponderá con la probabilidad de obtener cara (prob_0) y el segundo con la probabilidad de obtener cruz (prob_1). Si quisiéramos extraer, por ejemplo, prob_0 podríamos proyectar el vector ‘p’ sobre el primer eje. Esa proyección se corresponde con la matriz de transformación M_0 = 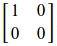. Si calculamos la longitud de la norma (l_{1}) del resultado de aplicar la matriz M_0 al vector ‘p’ obtendremos la probabilidad prob_0.

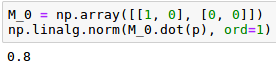
Para obtener la probabilidad de obtener cruz tendríamos que proyectar el vector ‘p’ sobre el segundo eje de la siguiente forma:

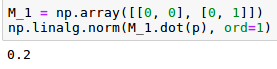
Esto nos lleva a la cuestión de cómo transformar una distribución de probabilidad en otra, por ejemplo, para cambiar el sesgo de una moneda.

Hemos visto que una distribución de probabilidad se puede representar como un vector estocástico y para modificarlo podemos multiplicar una matriz de transformación sobre dicho vector siempre que esa matriz cumpla unos requisitos:

  • Como son que cada una de sus columnas debe sumar 1 (la suma de todas las probabilidades debe ser 1).

  • Además debemos multiplicar esa matriz por la izquierda del vector.

Esta matriz recibe el nombre de left stochastic matrix. En el siguiente ejemplo veremos como transformar un vector estocástico ‘p’ correspondiente a una moneda no sesga (50% de probabilidad de obtener cara y 50% de obtener cruz) en otra que sí está sesgada después de multiplicar a ‘p’ por la izquierda por una left stochastic matrix:

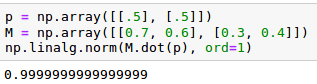
Para terminar este primer artículo, vamos a introducir el concepto de Entropía como medida de desorden o en nuestro caso, de falta de predictibilidad cuya definición formal será:

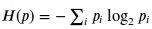
En el siguiente gráfico comprobaremos cómo la Entropía será máxima en el caso de una moneda no sesgada, que se corresponde con una distribución uniforme:

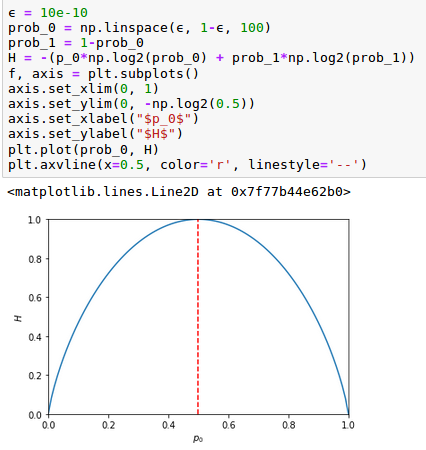
En siguientes artículos comenzaremos a movernos por el apasionante mundo de la Computación Cuántica haciendo paralelismos con los conceptos que acabamos de ver. ¡No te los pierdas!