Introducción A La Computación Cuántica Con Qiskit 2
En el primer artículo de esta serie se expuso cómo la unidad fundamental de información en sistemas de Computación Clásica era el bit y cómo se tratan las distribuciones de probabilidad en ese paradigma.
El objetivo de esta nueva entrega es el de ampliar nuestra perspectiva a la hora de abordar la modelización de problemas. Comencemos.
Qubits
La Computación Cuántica emplea, como se comentó anteriormente, principios presentes en física cuántica como los fenómenos de superposición y entrelazamiento, entre otros, para llevar a cabo cálculos de una forma más eficiente que con la computación tradicional. Esto lo consigue empleando como unidad de información el qubit, que es un sistema de mecánica cuántica de 2 estados, pero que cuando es observado y medido puede tomar cualquier posible combinación de esos 2 valores.
En el artículo inicial se presentó el ejemplo del lanzamiento de una moneda como un caso que podía modelizarse como una distribución de probabilidad en Computación Clásica y se representaba como un vector columnar.
Como primera aproximación podemos acercarnos al concepto de estado cuántico también como una distribución de probabilidad representada a través de un vector columnar que para identificarlo y distinguirlo del vector de Computación Clásica se empleará el denominado ket de la notación Dirac.
Siguiendo esta nomenclatura, el ket que representa el estado de un qubit se escribirá de la siguiente forma:
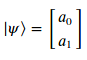
Donde (a_{0}), (a_{1\ } \in \text{\ ℂ}) y se denominan amplitudes de probabilidad de forma que cada amplitud estará asociada a un estado cuántico. La diferencia con el modelo clásico es que ahora el requisito de normalización es en la norma (l_{2}) en vez de en (l_{1}). Formalmente esto se traduce en que la raíz cuadrada de la suma de los cuadrados de los valores absolutos de las amplitudes será igual a 1:
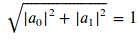
Profundizando en cómo representar un estado cuántico, hay que decir que se emplean como vectores de base canónica en 2 dimensiones los kets 0 y 1 cuya notación Dirac será la siguiente:
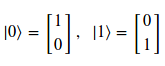
Combinando lo que hemos visto sobre cómo representar el estado de un qubit con la notación de la base canónica en computación cuántica, podemos describir el estado de dicho qubit (\psi)empleando esa base canónica de la siguiente forma:
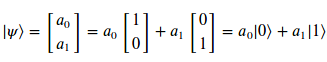
(\psi)
| La expansión del estado del qubit (\psi)en una base nos lleva a unos de los fenómenos más importantes en mecánica cuántica, la Superposición. Si observamos una muestra de esa distribución de probabilidad que representa el qubit y la medimos, obtendremos la salida ‘0’ con una probabilidad igual al cuadrado del valor absoluto de la amplitud que acompaña a la base canónica ket 0, es decir, ({ | a_{0} | }^{2}) y que obtendremos un ‘1’ con probabilidad ({ | a_{1} | }^{2}) (el cuadrado del valor absoluto de amplitud que acompaña al ket 1). Esta regla que nos permite calcular la probabilidad con la que se obtendrá cada uno de los estados cuánticos recibe el nombre de regla de Born. |
Circuitos Cuánticos con Qiskit
Como la idea es ir viendo cómo implementar estos conceptos de teoría empleando el framework Qiskit, vamos a comenzar simulando el ejemplo del lanzamiento de una moneda totalmente sesgada donde se obtendrá “cara” en el 100% de los lanzamientos, por lo que el ket 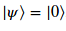
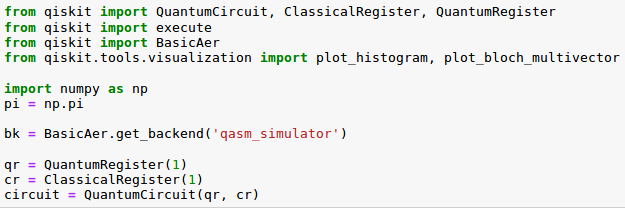
La librería ‘BasicAer’ proporciona un framework de simulación para la pila de software de Qiskit. En concreto, mediante su método ‘get_backed’ permite definir el entorno de ejecución que podrá ser o bien un simulador o un procesador cuántico real. En este caso, se está indicando que se utilizará el simulador ‘qasm_simulator’, por lo que la ejecución no se realizará en un entorno cuántico auténtico pero tratará de imitarlo y devolverá un diccionario con el contador de las medidas realizadas que estarán almacenadas en registros clásicos del circuito cuántico.
En la variable ‘qr’ se almacenará la referencia a un registro cuántico que permitirá almacenar un qubit. Mientras que la variable ‘cr’ se empleará para manejar un registro clásico que contendrá un bit. Por último, en la variable ‘circuit’ se define un circuito cuántico que inicialmente dispondrá del registro cuántico ‘qr’ y del registro clásico ‘cr’.
Hay que decir que cualquier qubit estará siempre inicializado por defecto en el ket 0 por lo que si lo medimos obtendremos el resultado deseado de una moneda totalmente sesgada que devuelva siempre ‘cara’. Para realizar esa medición emplearemos el método ‘measure’ del circuito cuántico que hemos definido en la variable ‘circuit’:

El método ‘measure’ recibirá el qubit que hemos almacenado en el registro cuántico ‘qr’, y cuando sea ejecutado el circuito, realizará una medición mediante la observación del estado cuántico lo que provocará que dicho estado colapse y se obtenga un valor concreto que será almacenado en el registro clásico definido en la variable ‘cr’.
Una vez que se ha añadido esa operación de medición al circuito procederemos a ejecutarlo 50 veces (parámetro shots=50) mediante la librería ‘execute’ de Qiskit almacenado la referencia a esa llamada en la variable ‘job’. Dicho método ‘execute’ recibirá el circuito a ejecutar y el backend de ejecución. Una vez hecho eso, se guardará en la variable ‘result’ la llamada al método ‘result’ del objeto ‘job’. Por último, como estamos empleando el ‘qasm_simulator’ dispondremos del método ‘get_counts’ para obtener un diccionario donde cada clave será un estado y su valor el número de ocurrencias del mismo durante los experimentos (shots). Podremos comprobar que las 50 veces que se repite la ejecución del circuito cuántico y se realiza su medición se obtiene siempre un ‘0’. Si estas ejecuciones se hubieran realizado en un procesador cuántico real podríamos encontrar que esos resultados no coincidirían exactamente con estas medidas debido entre otros factores al ruido.
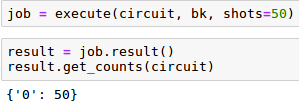
Acabamos de definir y ejecutar nuestro primer circuito cuántico para simular el problema del lanzamiento de una moneda sesgada. Y como probablemente os hayáis quedado con ganas de seguir jugando os emplazo al siguiente artículo de esta serie donde continuaremos profundizando en este apasionante campo.