Introducción A La Computación Cuántica Con Qiskit 3
En el primer artículo de la serie vimos cómo aproximarnos a las distribuciones de probabilidad en la Computación Clásica que emplea bits como unidad básica de información y en el segundo comenzamos a asomarnos de forma superficial a la Computación Cuántica introduciendo conceptos como qubit, base canónica, superposición, regla de Born y finalizamos viendo cómo implementar un circuito cuántico con Qiskit que modelizaba el problema del lanzamiento de una moneda completamente sesgada que siempre devuelve ‘cara’ (que se corresponde con el valor de salida ‘0’).
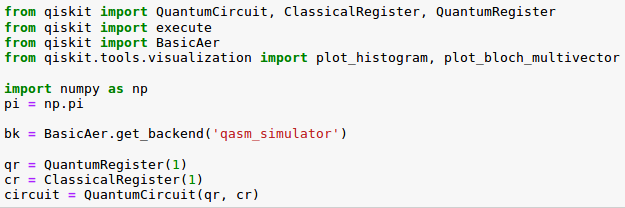
Utilizaremos ese código como punto de partida para los temas que vamos a tratar en esta ocasión:

Esfera Bloch
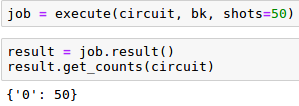
Al realizar en el backend ‘qasm_simulator’ las 50 ejecuciones y posteriores medidas del circuito anterior formado por un qubit inicializado en el ket 0 se obtiene siempre la salida ‘0’ (cara de la moneda).
Sería muy útil disponer de algún mecanismo de visualización para facilitar la comprensión de los pasos que vamos dando y aquí es donde entra en escena la Esfera Bloch. Se trata de una representación que permite proyectar un estado cuántico a una localización de la superficie de una esfera con unas características un tanto especiales.
Habíamos visto que un qubit tiene 2 amplitudes de probabilidad (una correspondiente a cada base canónica) y como son números complejos (parte real y parte imaginaria) se necesitaría un espacio de 4 dimensiones. Pero como los vectores están normalizados esto elimina un grado de libertad por lo que podríamos emplear una representación en 3 dimensiones, que como estaréis imaginando, será la Esfera Bloch.
| Antes comentábamos que esta esfera tiene una serie de peculiaridades. Su polo norte se corresponde con el estado del **ket | 0>** y su polo sur con el del **ket | 1>. Intuitivamente esto podría extrañar ya que en el eje Z se encuentran 2 vectores que son **ortogonales. La potencia de este tipo de representación es que cualquier punto de la esfera se corresponderá con un estado cuántico y también podemos afirmar que cualquier estado cuántico puro, es decir, un estado cuántico representado por un ket (vector columnar) se podrá visualizar como un punto de la esfera. También podremos encontrar estados cuánticos mixtos (no descritos por un ket) que estarán representados dentro de la esfera. |
| Ya es turno de volver a tocar un poco de código y ver cómo se visualiza esa Esfera Bloch. Para ello, en primer lugar vamos a emplear el backend ‘statevector_simulartor’ mediante llamada a BasicAer.get_backend(). A continuación, crearemos un circuito llamado ‘circuit’ formado por un registro cuántico (‘qr’) y por uno clásico (‘cr’). El objetivo es que el qubit almacenado en ‘qr’ se encuentre en el estado ket | 0> (situación que ocurre por defecto) y visualizarlo en la Esfera Bloch. Hay que decir que para modificar el estado de los qubits emplearemos puertas cuánticas (matrices que transformarán los vectores columnares de los qubits). En este caso no hay que realizar ninguna modificación al qubit pero aun así hay que añadir una operación llamada ‘iden’ al circuito que corresponde con la matriz identidad. |
Un punto a señalar es que por convenio en los registros cuánticos la posición menos significativa será la de más a la izquierda. Es decir, si se define un registro cuántico que contendrá 2 qubits:
qr = QuantumRegister(2)
| El qubit menos significativo, es decir qr[0], será el que esté más a la izquierda y el más significativo es de más a la derecha en la siguiente representación ** | 00>**. |
En el caso de los registros clásicos (en los que guardaremos los resultados de las mediciones de circuitos cuánticos) la posición menos significativa será la de más a la derecha como ocurre a la hora de representar bits.
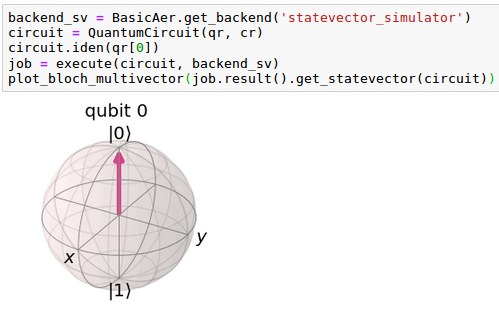
Volviendo a nuestro ejemplo, una vez añadida al circuito la operación ‘iden’ sobre el qubit se invocará al método ‘execute’ sobre el circuito indicando el backend almacenando el manejador de esa llamada en la variable ‘job’. Una vez hecho esto, se invocará al método ‘plot_bloch_multivector’ haciéndole llegar el resultado de ‘job.result().get_statevector(circuit)’.
| En la siguiente imagen puede verse el código completo y la visualización de la Esfera Bloch en la que aparece resaltada la flecha correspondiente al qubit en el estado del ket | 0>. |
Superposición
| Para entender el fenómeno de la Superposición vamos a seguir con el ejemplo del lanzamiento de una moneda pero ahora el objetivo es que no esté sesgada. Es decir, vamos a pasar del caso en que la moneda estaba completamente sesgada de forma que siempre se obtenía cara (ket | 0>) a la situación de que en el 50% de los casos se obtenga cara y en el otro 50% se obtenga cruz que se corresponderá con el estado de superposición (\frac{1\ }{})(( | 0 > + | 1 > ))donde |
| ({(\frac{1}{})}^{2})= (\frac{1}{2}) de los casos que según la regla de Born la salida se corresponderá con el ket | 0> y el resto al ket | 1>. |
Una forma de realizar esta transformación será empleando la Quantum Gate ‘ry’ que se corresponderá con una rotación de (\frac{\pi}{2})en el eje Y. Esa puerta se implementa mediante la matriz:
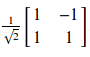
En futuros artículos de esta serie veremos más tipos de puertas cuánticas y entre ellas la puerta Hadamard que nos permitirá llegar también a un estado de Superposición.
| A continuación, veremos el código para construir el circuito que parte de un qubit en el estado ket | 0> , le aplica la puerta ‘ry’ para obtener una moneda no sesgada e invoca al método ‘plot_histogram’ sobre el resultado de 50 ejecuciones del circuito en el backend ‘qasm_simulator’ (almacenado en la variable ‘bk’) para poder obtener el conteo de veces en el que el lanzamiento de la moneda acaba en cada estado. |
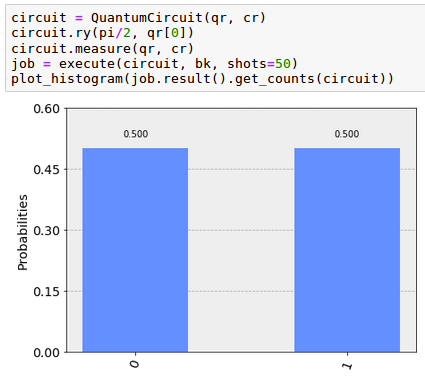
Si queremos visualizar ese experimento en la Esfera Bloch el código sería el siguiente
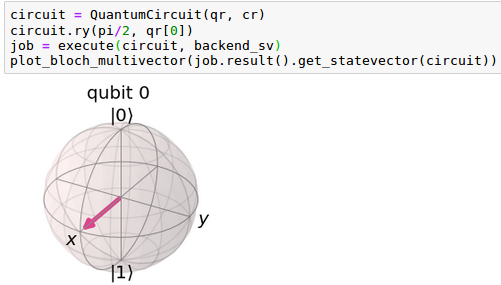
Como se puede comprobar se ha producido una rotación de 90º sobre el eje Y.
En el siguiente artículo seguiremos jugando con puertas cuánticas. ¡No os lo perdáis!