Introducción A La Computación Cuántica Con Qiskit 4
En el segundo artículo de esta serie se comentaba que las amplitudes de probabilidad son números complejos en contraposición con los números reales positivos que se emplean en Computación Clásica.
Superposición y números complejos
Los números complejos tiene la forma de a + bi donde ‘a’ es la parte real y ‘bi’ es la parte imaginaria siendo ‘a’ y ‘b’ números reales positivos o negativos e ‘i’ se corresponde con el número imaginario de forma que i = () (ya que no tenemos números reales que después de elevarlos al cuadrado sigan siendo negativos, por lo que no podremos volver hacia atrás haciendo la raíz cuadrada).
Los números complejos permiten representar coordenadas en un plano de manera que la parte real se asociará al eje X y la parte imaginaria con el eje Y. Por lo que sumar en la parte real supondrá movernos hacia la derecha, restar en la parte real movernos hacia la izquierda, sumar en la parte imaginaria nos permitirá desplazarnos hacia arriba y restar en la parte imaginaria supondrá movernos hacia abajo en el plano.
Suma / Resta de Números Complejos
(7 + 3i) + (3 - 5i) = (10 -2i)
Multiplicación de Números Complejos
(7 + 3i) * (3 -5i) = 7 * 3 + 7 * (-5i) + 3i * 3 + 3i * (-5i) = 21 + (-35i) + 9i + (-15(i^{2})) = 21 -26i -15*(-1) = 36 - 26i
La razón por la que (i^{2})simplifica a (-1) es porque i = () .
División de Números Complejos
Para realizar la división de números complejos hay que introducir el concepto de conjugada de números complejos, que consiste en cambiar el signo a la parte imaginaria. Por ejemplo la conjugada del número complejo (a + bi) será (a - bi). Multiplicar un número complejo por su conjugada supone que los términos centrales se cancelan:
(a + bi) * (a - bi) = (a^{2}\ - abi\ + \ abi\ - {(bi)}^{2})
Para realizar la división de números complejos multiplicaremos al numerador y al denominador por la conjugada del denominador:
(7 + 3i) / (3 - 5i) = ((7 + 3i) * (3 + 5i)) / ((3 - 5i) * (3 + 5i))
| Para comprobar la utilidad de emplear números complejos vamos a realizar un circuito cuántico que aplique una rotación ‘ry’ de 90º pero ahora al ket | 1>. |
| Hemos visto que todo qubit comienza inicializado en el estado ket | 0> por lo que tendremos que aplicar la puerta cuántica ‘x’ (que se correspondería con una puerta lógica NOT) sobre el qubit para que pase a estar en estado | 1>. |
La puerta cuántica ‘x’ se corresponderá con la matriz:

| Una vez que el qubit se encuentre en el | 1> aplicaremos la puerta ‘ry’ con un ángulo de 90º para realizar dicha rotación: |
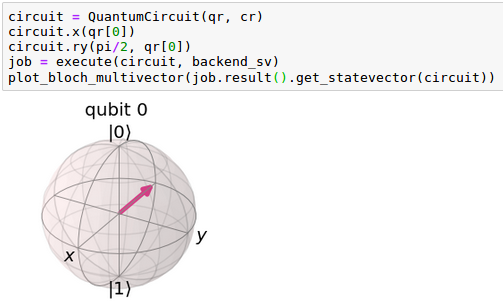
| En el tercer artículo de esta serie se aplicó la puerta ‘x’ sobre el qubit en el estado | 0> y el resultado fue: |
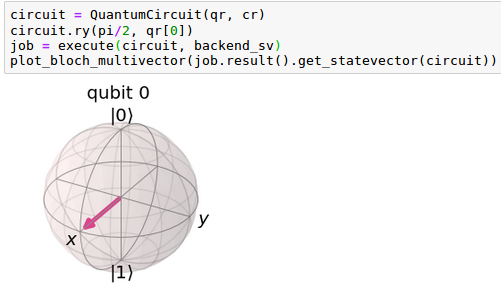
| Se puede comprobar que cuando se aplica la rotación ‘ry’ sobre el ket | 1> el resultado es similar al anterior pero con signo opuesto, por lo que tendremos una amplitud de probabilidad negativa. El estado obtenido será: |
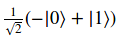
| La utilidad de disponer de números complejos para representar las amplitudes de probabilidad de los estados cuánticos se hace patente cuando se comprueba que el signo negativo del ket | 0> anterior no puede observarse al realizar la medición de las estadísticas de la ejecución del circuito cuántico. Para obtener dichas estadísticas de las frecuencias de cada resultado se ha empleado el backend ‘qasm_simulator’: |
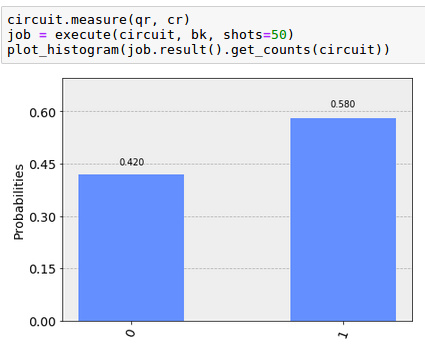
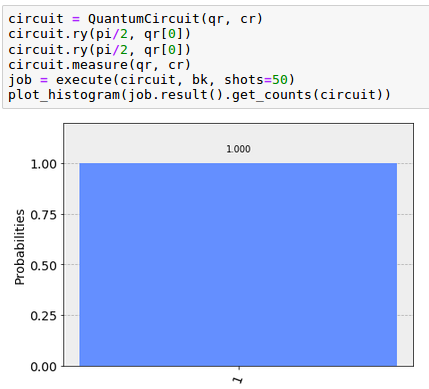
| Se puede comprobar que prácticamente se han producido el mismo número de caras (‘0s’) que de cruces (‘1s’). La utilización de números complejos permite modelar un fenómeno de mecánica cuántica conocido como ‘interferencia’ según el cual las amplitudes de probabilidad puede interactuar unas veces constructiva y otras destructivamente. Una forma de comprobarlo es aplicar sobre un qubit en el estado | 0> dos rotaciones ‘ry’ consecutivas de 90º. Al realizarlo obtendremos el ket | 1> aunque durante el proceso hubo cierta superposición. |
El código para realizar este experimento en el que se realizarán 50 ejecuciones del circuito cuántico sobre el backend ‘qasm_simulator’ y se obtendrá el histograma de los resultados es el siguiente:
 ()
()
En próximos artículos seguiremos avanzando tratando más propiedades presentes en mecánica cuántica como por ejemplo el ‘Entanglement’ y viendo cómo implementarlas empleando el framework Qiskit. ¡Os esperamos!