Introducción A La Computación Cuántica Con Qiskit 5
En el cuarto artículo de esta serie se introdujeron conceptos como superposición e interferencia y cómo codificarlos empleando Qiskit. Ahora es turno de ver cómo representar varios qubits y de adentrarnos en la propiedad conocida como entanglement.
Múltiples qubits
En este punto vamos a empezar a trabajar con estados cuánticos formados por varios qubits. Si recordamos lo que vimos anteriormente, un estado cuántico lo podemos asemejar a una distribución de probabilidad y un qubit es un estado cuántico de 2 niveles [a0, a1], de forma que podemos representar un estado cuántico mediante un vector columnar.
| Para hacer referencia a su label (el nombre de dicho estado) se utilizará lo que se denomina ket en la notación Dirac, es decir, podemos referirnos a nuestro estado cuántico mediante el ket ( | \psi >). Para continuar refrescando conceptos previos, estas distribuciones de probabilidad deberán tener norma 1 en la norma L2. |
Por tanto recapitulando, podemos escribir un qubit de la siguiente forma:
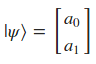
Donde a0 y a1 reciben el nombre de amplitudes de probabilidad y son números complejos, por lo que no sólo estaremos restringidos al cuadrante positivo del plano como ocurría con las distribuciones de probabilidad clásica cuya norma debe ser igual a 1 en la norma L1 y además cada probabilidad debía ser mayor o igual a 0 (lo que únicamente permitía representaciones en el cuadrante positivo citado anteriormente).
Como en computación cuántica el requisito de normalización debe ser la norma L2 eso puede formalizarse para el caso de un qubit en que:
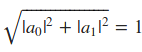
Podemos encontrar 2 qubits especiales llamados vectores de base canónica en 2 dimensiones que son:
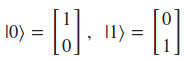
La parte interesante es que podemos expandir cualquier qubit en esta base de la siguiente forma dando lugar al fenómeno de superposición:
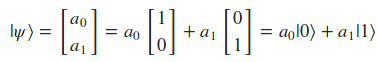
| Según la regla de Born, si extraemos una muestra del qubit ( | \psi >)obtendremos la salida 0 con una probabilidad ({ | a_{0} | }^{2}) y la salida 1 con una probabilidad de ({ | a_{1} | }^{2}). |
Una vez finalizado este repaso, toca ponernos manos a la obra con nuevos conceptos. Vamos a comprobar cómo añadir más qubits nos permite introducir otro fenómeno cuántico.
| En este punto nos puede surgir la duda sobre cómo representar en forma de vector columnar 2 qubits. La forma de hacerlo es empleando la operación de producto de tensores o producto Kronecker. Para entenderlo vamos a ver un ejemplo en el que partimos de 2 qubits ( | \psi >)y ( | \psi’ >): |
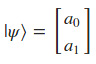
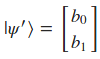
El producto de tensores o producto Kronecker de esos 2 qubits será:
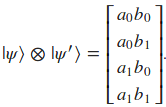
| Vamos a concretar un poco más. Supongamos que tenemos almacenado en el registro cuántico qr0 un qubit que está en el estado | 0> y también disponemos de otro registro cuántico llamado qr1 que de forma similar al anterior almacena un qubit en el estado | 0>. Una forma de visualizar la regla del producto Kronecker de esos 2 qubits ( | 0> (\otimes) | 0>) sería mediante el siguiente código: |
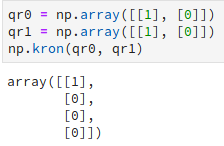
| El estado resultante del producto Kronecker de esos dos qubits que cada uno de ellos se encuentra en el estado | 0> se suele representar como | 00>. Si quisiéramos representar los estados | 01>, | 10> y | 11> tendríamos que seguir el mismo procedimiento que hemos realizado para generar el ket | 00>. |
| Hay que señalar que los estados | 00>, | 01>, | 10> y | 11> forman los vectores de base canónica en un espacio de números complejos de 4 dimensiones denotado como  |
Cuando empleamos modelos de Machine Learning y Deep Learning también trabajamos con espacios de alta dimensionalidad pero no se construyen como un producto de tensores sino que suele tratarse de (R^{n}), es decir, un mapeo a los números reales para alguna dimensión ‘n’.
El efecto de construir espacios de alta dimensionalidad empleando producto de tensores es que no todos los vectores de dicho espacio pueden ser escritos como el producto de vectores de los elementos de ese espacio. Este hecho que en principio puede parecer confuso, nos permitirá descubrir la propiedad cuántica conocida como entanglement, que recorreremos en el siguiente artículo viendo cómo la podemos observar empleando Qiskit. ¡No te lo pierdas!