Introducción A La Computación Cuántica Con Qiskit 6
En el quinto artículo de esta serie hicimos un repaso general de los conceptos más importantes desarrollados hasta ese momento, poniendo especial foco en cómo codificar 1 qubit. Eso nos llevó a plantearnos cómo se conseguiría llevar a cabo la representación de estados cuánticos compuestos por varios qubits, lo que a su vez abrió el camino para el tema en el que vamos a centrarnos en esta publicación: el fenómeno conocido como entanglement. Vamos a incorporar un concepto más a nuestra mochila. ¡Pero tranquilos que no será nada pesada!
Entanglement
| Vamos a comenzar de la misma forma que lo hicimos en el artículo anterior, recapitulando los puntos claves que se trataron en él. El primer tema que pudimos comprobar fue que la forma de construir estados cuánticos formados por varios qubits era mediante la operación del producto de tensores o producto Kronecker de los qubits individuales. Suponiendo que tenemos 2 qubits llamados ( | \psi >) y ( | \psi’ >): |
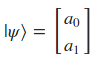
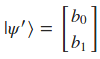
El resultado de realizar el producto de tensores o producto Kronecker de esos 2 qubits será:
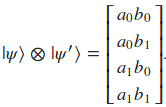
| Si estamos trabajando con estados cuánticos compuestos por 2 qubits entonces tendremos los siguientes vectores de base canónica: | 00>, | 01>, | 10> y | 11> en un espacio de números complejos de 4 dimensiones  |
También introdujimos en el artículo anterior la idea de que cuando construimos espacios de alta dimensionalidad empleando la operación del producto de tensores de los qubits individuales no todos los vectores de ese espacio resultante pueden ser obtenidos mediante el producto Kronecker de sus componentes.
| La mejor forma de entender algo es mediante ejemplos y por ello vamos a intentar demostrar ese concepto partiendo del siguiente estado de superposición de los kets | 00> y | 11>: |
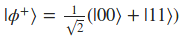
| Como el vector resultante es una combinación lineal de 2 de los vectores canónicos ( | 00> y | 11>) del espacio de los números complejos de 4 dimensiones, podemos decir que este vector pertenece a dicho espacio de  El problema es que esto no puede ser escrito como el producto Kronecker ( El problema es que esto no puede ser escrito como el producto Kronecker ( |
\psi > \otimes | \psi’ >) para cualesquiera 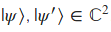 . . |
Para demostrarlo, vamos a escribir el estado cuántico 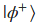 como un producto Kronecker de sus componentes y posteriormente vamos a expandir el resultado sobre los vectores de base canónica de los complejos de 4 dimensiones:
como un producto Kronecker de sus componentes y posteriormente vamos a expandir el resultado sobre los vectores de base canónica de los complejos de 4 dimensiones:
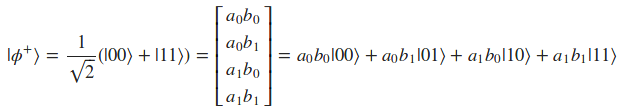
| Podemos ver que no aparecen los kets | 01> ni | 10> en esta parte de la expresión: |
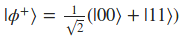
Por lo que llegamos a la conclusión de que (a_{0}b_{1} = 0) y (a_{1}b_{0} = 0). El problema es que eso lleva a una contradicción ya que como (a_{1}b_{1} = 1)de ahí extraemos que (a_{1})no puede ser 0 por lo que deducimos que (b_{0})debe ser 0. Pero eso tampoco puede ser posible debido a que como (a_{0}b_{0} = 1)entonces (b_{0})no podría ser 0.
Esto nos lleva a que los estados que no pueden ser escritos como un producto de tensores reciben el nombre de entangled states o estados entrelazados. Se trata de un fenómeno físico que indica fuertes correlaciones entre variables aleatorias, por ejemplo, 2 qubits aunque dichos qubits estén separados por grandes distancias, de forma que estas correlaciones no son explicadas mediante la mecánica clásica. Esta propiedad nos permite entre otras cosas poder medir uno de los qubits entrelazados e instantáneamente poder determinar el valor del otro aunque ese otro qubit se encuentre en un estado probabilístico.
A continuación, vamos a ver cómo crear el estado 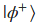 empleando Qiskit:
empleando Qiskit:
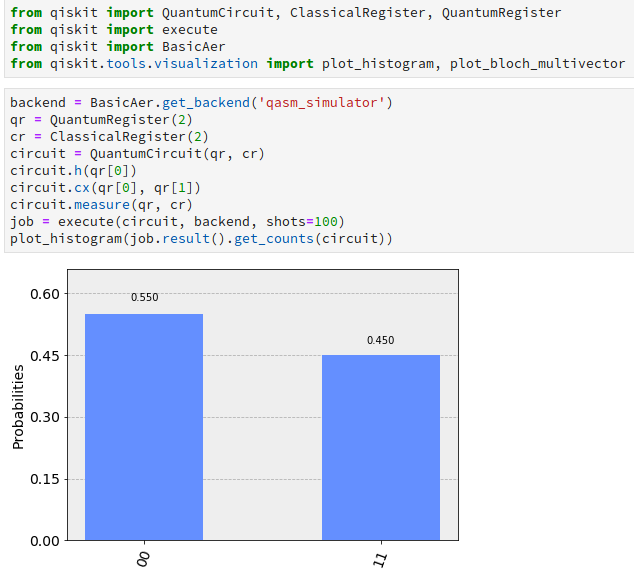
| En este ejemplo, disponemos de 2 registros cuánticos qr[0] y qr[1] cada uno de ellos inicializado por defecto en el ket | 0> y de 2 registros clásicos cr[0] y cr[1]. Creamos un circuito cuántico que dispone de esos 2 registros cuánticos qr y de los 2 registros clásicos cr. Una vez realizadas esas definiciones, aplicaremos la puerta Hadamard sobre el qubit 0 (el de más a la izquierda) siendo su definición: |
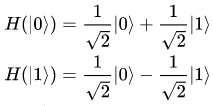
Su definicón gráfica y su matriz son las siguientes:
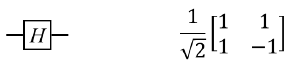
El estado parcial después de aplicar esa puerta Hadamard sobre el qubit 0 será
| (\frac{1}{})( | 00> + | 10>). |
A continuación se aplicará sobre el resultado del paso anterior la puerta cx o también conocida como CNOT o controlled NOT. Esta puerta emplea 2 qubits, uno de control y otro denominado target, de forma que si el qubit de control es 1 entonces aplicará la puerta NOT o también conocida como x sobre el otro qubit (target). El efecto que provoca es el siguiente en caso de que el qubit de control sea el de más a la izquierda:
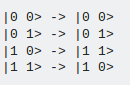
Y aquí podemos ver su definición en forma de matriz y gráfica:
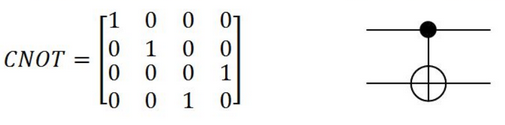
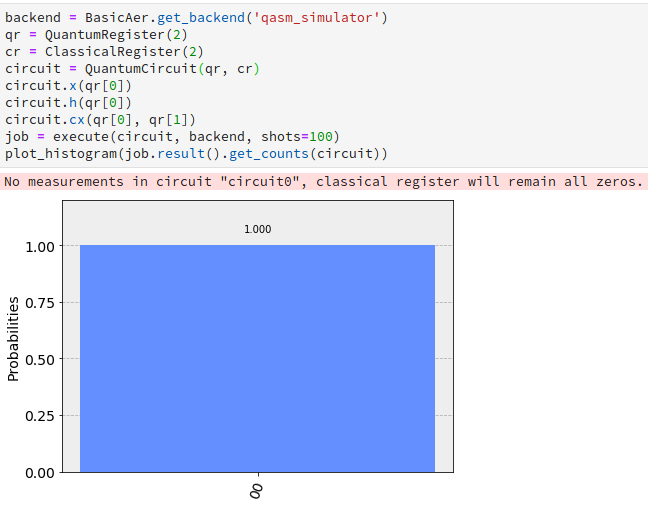
| Por lo que el resultado después de aplicar la puerta cx será (\frac{1}{})( | 00> + | 11>) estando los estados | 00> y | 11> en superposición. Esto puede comprobarse en el histograma donde cada uno de los estados aparece aproximadamente la mitad de las 100 veces (parámetro shots) que se repite la ejecución del circuito cuántico. |
Siguiendo este procedimiento vamos ver cómo se implementaría el estado:
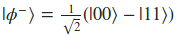
Hasta aquí este artículo en el que además de trabajar con estados formados por varios qubits y de introducir el concepto de entanglement hemos empezado a modificar estados empleando algunas puertas cuánticas. En los siguientes artículos profundizaremos en las distintas puertas cuánticas disponibles y cómo emplearlas usando el framework Qiskit. ¡No os lo perdáis!